---

Activity overview

Mathematical Modelling and Analysis 1 (MMA1) is a 10-week foundational mathematics course taken by almost all first-year undergraduates – totalling around 1000 in 2021/21 – in UCL’s school of engineering (UCL Engineering).  MMA1 seeks to engage students with the applications of mathematics and equip them to use mathematical ideas and language to model authentic engineering and societal problems.

In 2014, UCL Engineering launched the Integrated Engineering Programme (IEP), a radically redesigned undergraduate curriculum that emphasises multidisciplinary learning and the application of students’ engineering learning to real-world problems.  While the IEP prompted systemic changes to the first-year mathematics course, concerns remained about its excessive focus on abstract theoretical concepts (leaving some students unable “to apply their mathematical knowledge in the third or fourth year”) and its fragmented approach (with instructors from different departments lecturing on a new topic each week with limited integration to connect students’ learning).  Calls for reform to this course grew over the seven years that followed.  However, the logistical challenge of coordinating a common way forward across eight^[1] separate departments stymied action.  The move to emergency online teaching at UCL, however, offered an opportunity to consolidate and accelerate plans for fundamental change.  In the words of the course lead: “if we’re going to take this online, we’re going to do it as well as UCL possibly can… let’s take the best out of a terrible situation and make something that we are proud of”.  

What emerged was a root-and-branch reform to the course focus, structure and pedagogy.  MMA1 is structured around 10 week-long scenarios.  Each week, students are asked to “start by observing the real world” as they are introduced to a new authentic application – such as the economics of family-run coffee plantations in Brazil – before exploring the mathematical concepts that could be used to model and investigate it – in this case, calculus.  The synergy between each application and associated concept is explored throughout the week, culminating in a group activity where students are asked to develop a mathematical model to describe the real-world scenario, such as air pollution or non-invasive surgery.  

The course is structured around three components:

1. Fundamentals: an optional, self-paced component designed to ensure that students are equipped with the prerequisite mathematical capabilities to tackle the Core Topics;
2. Core Topics: the major focus of the course that explores a new mathematical concept each week, such as complex numbers or integration, together with a linked real-world ‘scenario’;
3. Computational Modelling: to support students’ learning of the Core Topics, they are asked to model the mathematical concepts and scenarios using the programming language MATLAB.

Each week, a new ‘scenario’ and mathematical concept are threaded across each of these components and throughout the course’s asynchronous and synchronous activities.  This connectivity is designed to help students contextualise, explore and integrate their learning.

---

^[1] Please note: UCL Engineering is home to 10 departments in all; students from eight departments participated in MMA1. 

---

Independent review

Distinctive features

Although the look and feel of MMA1 is very different from a typical mathematics foundation course, what most sets it apart is its success in setting mathematics in an authentic and relatable context where it can be used to model and explore students’ observations of the real world.  The course lead is a driving force behind this approach.  He explained how he had been influenced by his experience as a mathematics teacher to disadvantaged children in Brazil, where he had, in his own words:

“captured [children’s] attention with mathematics by showing them that mathematics is a language that they can use… [to] take a look at the world around them and describe these physical phenomena with mathematical variables and operations, to make simple models… The connection needs to not only be intellectual, there needs to be a human connection”.

This approach of asking students to build models that explain and explore “problems related to humanity” is infused throughout the course, with the complexity of challenges building progressively over the 10 weeks. There is, of course, a risk that such attempts to contextualise mathematical learning in real-world applications will introduce artificial constructs into a course that distract from students’ learning rather than add to it. The question of whether these scenarios felt ‘contrived’ was therefore addressed explicitly during the interview process. Student feedback, however, was unequivocal and suggested that this approach was both “genuinely interesting, genuinely fun” and offered a platform to explore, apply and deepen their learning. Interviewee feedback from instructors similarly pointed to a clear link between high levels of student engagement and both the relatability and societal relevance of the ‘scenarios’ integrated into MMA1. In the words of one teaching team member:

“the students were really surprised, realising I can actually change things.  You know, I can actually plan a protocol for a non-invasive surgery.  I can design a microphone.  I could help a farmer to maybe one day to get to more profit.  It’s really connecting science to the individual, making engineering more human and more personal… the students came in with a lot more excitement”.

Some interviewees also went on to suggest that the course had helped to broaden students’ perceptions of mathematics from being a rigid method that only offered “just one right answer” to a tool that is used by engineers to investigate observed phenomena and explore new ideas, and where the solutions developed are open to discussion and debate.  One student spoke about the realisation amongst his group of friends on the course that they had all taken strikingly different approaches to the same coursework problem: “it was so different for everybody, but it was not wrong.  You could see the logic, but it was amazing how we had used tools so differently on the same topic”.

Success factors

As noted in Section 2.1, a particularly striking theme of interviewee feedback was the perceived high levels of student engagement with the course.  One departmental lead characterised this as, “not just passive engagement, like going to lectures and waiting for things to happen, but an actual active engagement with the material”.  Fostering such high levels of engagement was by no means guaranteed, particularly for a foundational mathematics course that brings together a large and diverse student cohort from across a range of disciplines.  Indeed, the previous version of the course was long associated with poor student feedback and low engagement, and some in the teaching team feared that the fully online delivery in 2020/21 would only exacerbate the challenges faced.  The “overwhelmingly positive” student response to MMA1 therefore came as something of a surprise to many.  There appeared to be several factors underpinning high student engagement.  Undoubtedly, the first was the contextualisation of students’ learning in real problems, as described in Section 2.1.  However, a number of other factors also appeared to be crucial, including the course offering:

• a clear, coherent and active approach: the course design, as delivered through the learning platform Moodle, was described as setting “a benchmark for other courses” in UCL Engineering.  Structured week-by-week, the online information offered students clarity on the structure, focus and expectations of the course in a way that allowed them to plan their time and monitor their progress.  Considerable expertise and care were also devoted to embedding active learning into both the synchronous and asynchronous components of the course and establishing a clear connection between each of these activities.
• responsiveness to student feedback: two mechanisms were established to provide appropriate and rapid feedback to students’ questions while working asynchronously.  Firstly, an automatic marking system was established for MATLAB coursework that provides students with immediate feedback on their work, including explanations relating to common errors.  Secondly, an online Moodle forum was established where post-graduate teaching assistants (PGTAs) provided rapid and detailed responses to questions posed by students throughout each week.  Student feedback suggested that, although not all posted questions on the forum themselves, a large proportion regularly reviewed the threads of questions and responses.
• small group learning: despite the large cohort size (of around 1000 students), all synchronous workshops were based around learning in relatively small groups of 45–50.  Students remained in the same departmentally-based group for all ‘live’ sessions throughout the course, in which they were able to build networks and friendships: “it is a huge [course]… but they are not looking out at a sea of students… they are working with a small group of friends”.   
• engaging students from all backgrounds: a major criticism of the previous mathematics course was that it did not “provide a level playing field for students coming in from different backgrounds”.  It neither offered support to students without the required prerequisite mathematics high school attainment (this learning was delivered through a separate ‘remedial’ mathematics programme) nor provided opportunities to extend the learning of students with a strong mathematical background.  In contrast, interview feedback suggested that MMA1 offered an enriching learning experience for students of all mathematical aptitudes, including those at either end of this distribution.  The optional ‘foundational’ component supported students’ self-paced learning in the key mathematical course prerequisites, without calling for them “to identify themselves as needing extra help” by signing up for ‘remedial’ sessions.  The application of mathematics to model real societal and engineering problems, accompanied by training in MATLAB, was also understood to “offer something completely new for the high achievers in mathematics” to extend their learning. 
• avenues for collaboration: MMA1 offered a number of different avenues for student-led learning and collaboration, such as via the online forum (to discuss and debate questions), the online ‘share boards’ (where students could share ideas and solutions asynchronously), and the group activities during the ‘live’ workshops (to develop and explore mathematical models).

While undoubtedly the product of committed collaboration of instructors from across UCL Engineering, the success of MMA1 in establishing each of these components was underpinned by two key factors.

The first was the coherence of vision adopted for the course, which was driven by two individuals: the course lead and the school’s learning technologist.  Each brought considerable pedagogical experience – both, interestingly, with backgrounds as high-school teachers – and were given the autonomy to design much of the course’s structure and focus from a blank slate.  A crucial outcome of this collaboration was the identification of 10 real-world applications that punctuated the course: to ensure that each of these scenarios offered an appropriate balance of societal relevance and applicability to the mathematical concept in question, while at the same time connecting with each of the eight engineering disciplines represented by MMA1 student participants.  The “active flipped learning” approach taken by MMA1 – one that connects the synchronous and asynchronous learning through a real-world “hook that engages the students’ imagination” – also drew upon a model that had previously been validated by the school’s learning technologist within UCL’s school of management.  

The second success factor was the disruption imposed by emergency teaching.  Not only did this provide the conditions for collective and abrupt change to the course, it also enabled access to additional resources for the transition to online learning, including the allocation of a significant number of additional PGTAs and dedicated support from the school’s learning technologist.  One interviewee described the development of MMA1 as the product of: “a lot of personal and institutional investment by all concerned. It was the sort of investment departments and individual academics would not necessarily consider if there was no pandemic”.  The outcome, however, provides a clear demonstration of what can be achieved through a blended approach when a unified and coherent vision is applied and dedicated resources and expertise are made available.  That the concept was proven in a course such as foundational mathematics – long associated in universities worldwide with logistical complexity and low student engagement – is likely to turn heads across the engineering education sector.

Challenges faced

Interview feedback suggested that MMA1 faced a number of challenges.  

Some challenges were associated with the design and development of the course, and the logistics of coordinating an educational change that encompasses eight distinct departments during a global pandemic. The development of the virtual learning environment was non-trivial, and called on a significant investment of time and expertise by the school’s learning technologist.  In addition, some members of the teaching team initially expressed deep concerns about driving a change of such magnitude “in a year when I am already anxious, when I want to hold onto things I know”.  Considerable time was devoted to cross-departmental discussion, to build cohesion across the teaching team, explore the vision for the course and allay concerns that students would not engage with the scenarios or the asynchronous activities.  This teaching team met regularly before and throughout the course to, in the words of one member, “support each other and share best practice”.  It was noted that, by the third or fourth week of delivery of the course, the teaching team had developed a high level of cohesion and trust, with some reporting feeling empowered “to be more ambitious” in workshops in their own departments based on the experiences of and approaches taken by others.

Interview feedback also pointed to a range of challenges associated with the course delivery, such as connecting students across different time zones for synchronous collaboration.  However, the challenges repeatedly highlighted by interviewees related to fostering student connectivity and active interaction when learning exclusively online.  For example, members of the teaching team pointed to the difficulties they had faced in identifying students “that are struggling, but are not saying anything” within an online environment.  In the words of one PGTA:

“normally you can see those people in the classroom and you can go over to them and talk to them and help them, and they will engage with that.  But it’s much harder to get to those students this year [during fully online delivery]… because you don’t have that in-person interaction, you cannot see their faces and if they won’t ask questions, it’s much harder to get to those students”.

Student interviewees similarly spoke about the challenge of connecting with peers when web-cams were switched off.  One student contrasted his experience of productive, collaborative group working in most weeks when “everyone was on camera” with one particular week when he was allocated to a group where “no one had their camera on, and no one spoke.  We all just ended up working on our own in silence”.   Interviewee feedback suggested that the “student culture for having cameras switched on” varied considerably by department.  However, the number of MMA1 students opting to keep their cameras turned on during the synchronous workshop sessions reduced progressively throughout the 10-week course in almost all departments.  This problem was replicated in courses throughout UCL Engineering (and, indeed, throughout other engineering schools worldwide) over the course of emergency teaching.

---

Activity details

MMA1 is a mandatory first-year course for UCL Engineering undergraduates, scheduled in the first term of study.  It is a 15-credit course (out of 120 credits allocated to the full academic year), equating to 150 hours of learning over the full academic year (including assessments and exams in the second and third terms).

Participants and project groups

Around 1000 students participated in MMA1 in 2020/21.  This cohort was divided into sections of 40–50 students, all from the same department, for all synchronous ‘live’ workshop activities.  For group activities, each section was further divided into different groups each week, each of 5–6 students.

Structure of the activity

The 10-week course is structured around a new mathematical topic and connected real-world scenario each week.  So, for example, in the fourth week of the course, complex numbers are explored in the context of microphone design; and in the seventh week, differential equations are used to study the energy balance model of climate change around the planet earth.

Within this week-by-week structure, the course brings together three components: Fundamentals, Core Topics and Computational Modelling.  As illustrated in Figure 1, each component includes synchronous and asynchronous elements and is supported by an online Moodle ‘forum’ where students can post questions throughout the week (with responses provided by PGTAs and peer students).  Further information about each component is summarised in the table below.

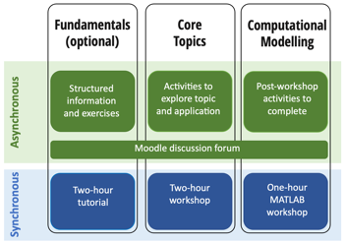
Fundamentals	This optional and self-paced component supports students’ learning in the prerequisite mathematical concepts used in the course, and ensures that all students are able to engage fully with MMA1, regardless of their mathematic backgrounds.  A 90-minute ‘diagnostic test’ at the beginning of the course allows students to self-assess their background mathematical knowledge and identify any particular areas of weaknesses.  The Fundamentals component brings together preparatory information and exercises (delivered asynchronously) with a ‘live’ tutorial session to address specific questions students may have.  Although the Fundamentals component of MMA1 is optional, over 50% of students opted to participate during the 2020/21 course.
Core Topics	Each week, students are introduced to the new application and mathematical topic through a series of asynchronous activities (such as videos, quizzes, polls and exercises) designed to take around three hours to complete.  These, for example, might include a short video introducing the primary factors influencing climate change, or a request for students to post examples on a ‘share board’ of consumer products that utilise complex numbers in their design.The weekly two-hour ‘live’ workshops are designed to analyse and apply what students have learnt in the asynchronous activities.  The departmental lead opens the workshop with a broad description of the mathematical topic and application, interspersed with outcomes from the online quizzes that students completed during their asynchronous learning to explore the ideas and discuss any common errors made.  After working on some simple problems individually, students are then divided into groups of five or six to tackle a challenge that brings together their learning for the week (see Section 3.3 for examples).
Mathematical Modelling	Using the programming language MATLAB, this course component supports the development of students’ programming and modelling skills.  It is designed to help students visualise and model real-world problems.  For example, one exercise was to predict the time it would take to clear a lake of water pollution.  ‘Live’ workshops open with an introduction to a different feature of MATLAB each week.  Students are then asked to apply these principles to a series of problems that are completed asynchronously, following completion of the workshop.

It should be noted that, once emergency teaching restrictions are lifted at UCL, it is envisaged that the two-hour synchronous ‘core topics’ workshop will be held face-to-face, but most other activities will continue to be delivered online.

The challenge brief

Each week of MMA1 culminates in a group activity that brings together a mathematical concept and real-world scenario.  The table below provides examples of group activities taken from two particular weeks in the course: week 5, which focuses on derivatives, and week 6, which focuses on integrals.

Week.5

In week 5, the concept and application of derivatives are explored in the context of family-run agriculture in Brazil.  The mathematical tools needed to describe and optimise systems that change as a function of one or several variables are taught using differential calculus.  During the synchronous workshop, students are asked to design coffee plantation zones that maximise the farmed area while minimising the perimeter, such that small-scale family-based farmers can optimise their production. For the group activity, students are challenged to develop and explore a mathematical model that describes the profit made by a small coffee grower.  Using the product price for two types of coffee (Arabica and Robusta) as working variables, a number of constraints for the problem are defined, such as production costs and a maximum joint production capacity for both species of coffee.  Groups are asked to identify the optimal prices that should be charged by farmers that allow them to maximise their profits within the problem constraints.

Week.6

In week 6, students study the concept of integrals through investigating heat deposition in non-invasive surgery techniques like Laser or High Intensity Focused Ultrasound surgery.  The fundamental theorem of calculus is explored through simple models of temperature change and heat deposition.  During the synchronous workshop, students are asked to calculate the temperature rises induced by a range of heating patterns, comparing the effects of linear and non-linear heating rates to the final temperature of a surgical target. For their group activity, students are challenged to solve a mathematical model that describes the extent of thermal ablation in biological tissue created by High Intensity Focused Ultrasound surgery.  Deducing from experimental observation that cell viability has a breaking point at temperatures above 43°C, groups are asked to apply integration techniques to calculate the thermal dose created from the linear heating of a tissue sample and estimate the resulting tissue ablation.

Learning goals/objectives

The learning goals for MMA1, as articulated in the course outline, are to:

• recognise how mathematical ideas are embedded in engineering contexts;
• represent real-world engineering systems in a mathematical framework;
• identify and draw upon a range of mathematical concepts, including Calculus, Linear Algebra, Differential Equations and Statistics to analyse specific problems and identify the appropriate mathematics to realise a solution;
• employ appropriate computer modelling techniques to efficiently solve and evaluate the performance of engineering systems;
• relate the behaviour of the output of mathematical models to the underlying physical or conceptual models of interest;
• carry out engineering problem-solving both collaboratively in a team and independently;
• present and interpret mathematical results in effective and appropriate ways to varied audiences, including non-mathematical engineering audiences.

Assessment

MMA1 incorporates both formative and summative assessment.  

The formative assessment is embedded in the asynchronous materials (via quizzes) and synchronous activities and problems during the synchronous ‘live’ workshops.  In most cases, students are provided with instant feedback on these assessments.

All summative assessment is mandatory and connected to the Core Topics element of the course.  For the 2020/21 course, it brought together three elements that spanned the full academic year:

• individual coursework (40%): students were asked to complete two items of individual coursework during the 10-week course that assessed their technical skills, creativity and programming skills.  Both items were set in the context of the weekly ‘scenario’, with students asked to develop models to explore the real-world problem. One piece of coursework, for example, looked at the levels of water pollution in a lake ecosystem and asked students to “derive an expression for the time that the authorities have to act for the clearing of the lake”.
• 24-hour exam (30%): at the close of the academic year, students took an ‘open book’ exam designed to assess their mastery of the core mathematical concepts.  The exam was designed to be two hours in duration, undertaken online over a 24-hour period.
• individual project (40%): following the completion of the course, students were asked to complete a four-week project designed to synthesize their learning and apply this to an in-depth scenario.  The project focused on the impact of climate change on the Great Lakes, a chain of freshwater lakes in the US.  Students were asked to create a water balance model that could be used to inform government policy for climate change.  Although this project was set as an individual piece of work in the 2020/21 course, the intension is for this to become a group project in future academic years. 

The teaching team

The teaching team for MMA1 in 2020/21 consisted of over 60 individuals and comprised: 

• the course lead (who: co-led the design and development of the course; and co-led the development and roll-out of training for the teaching team);
• the school’s learning technologist (who: co-led the design and development of the course; co-led the development and roll-out of training for the teaching team; led the development of the MMA1 learning management platform).  He was supported by two other learning technologists to support the student and staff experience of the online platform;
• five academics from across UCL Engineering (who: co-developed the asynchronous material associated with the mathematical Core Topics and one or more of the weekly ‘scenarios’; and led one or more ‘live’ workshop each week);
• twelve academics from the 8 departments on MMAI (who: led facilitation of the ‘live’ weekly workshops for students in their department and mark assessments);
• 40 PGTAs (who: facilitate the ‘live’ weekly workshops, for both the Core Topics and Computational Modelling; co-develop the MATLAB exercises; mark coursework; and post responses to students’ questions posted on the online Moodle forum).

All members of the teaching team met online on a weekly basis during the course design and preparation phase (from July to September 2020) and during its synchronous delivery phase (from September to December 2020) where they were able to discuss any particular challenges faced. 

The teaching team was offered a two-hour training programme in advance of the course (in addition to the mandatory IEP training for all PGTAs).  The MMA1 training, in which most members of the teaching team participated, provided an overview of the priorities for each element of the course and explored key topics in online teaching and learning, such as how to build student engagement online. 

Technology used

The following applications were used in the 2020/21 MMA1 course: 

• almost all synchronous and asynchronous learning materials were delivered through the learning management systems Moodle;
• the programming language MATLAB was used for computer modelling in conjunction with ‘automated’ online feedback provided through Grader.